User Guide > Using FlexPDE in Three-Dimensional Problems

We have stated that the layer interfaces need not be planar. But FlexPDE makes some assumptions about the layer interfaces, which places some restrictions on the possible figures.

•	Figures must maintain an extruded shape, with sidewalls and layer interfaces (the sidewalls cannot grow or shrink)

•	Layer interface surfaces must be continuous across region boundaries. If a surface has a vertical jump, it must be divided into layers, with a region interface at the jump boundary and a layer spanning the jump. (Not this: but this: )

•	Layer interface surfaces may merge, but may not invert. Use a MAX or MIN function in the surface definition to block inversion.

Using these rules, we can convert the canister of our example into a sphere by placing spherical caps on the cylinder.

The equation of a spherical end cap is

Z = Zcenter + sqrt( R^2 – x^2 – y^2)

Or,

Z = Ztop – R + sqrt(R^2 – x^2 – y^2)

•	To avoid grazing contact of this new sphere with the top and bottom of our former box, we will extend the extrusion from –1 to 1.

•	To avoid arithmetic errors, we will prevent negative arguments of the sqrt.

Our modified script now looks like this:

TITLE 'Heat flow around an Insulating Sphere'

COORDINATES

Cartesian3

VARIABLES

Phi { the temperature }

DEFINITIONS

K = 1 { default conductivity }

R = 0.5 { sphere radius }

{ shape of hemispherical cap: }

Zsphere = sqrt(max(R^2-x^2-y^2,0))

EQUATIONS

Div(-k*grad(phi)) = 0

EXTRUSION

SURFACE 'Bottom' z=-1

LAYER 'underneath'

SURFACE 'Sphere Bottom' z = -max(Zsphere,0)

LAYER 'Can'

SURFACE 'Sphere Top' z = max(Zsphere,0)

LAYER 'above'

SURFACE 'Top' z=1

BOUNDARIES

REGION 1 'box'

START(-1,-1)

VALUE(Phi)=0 LINE TO (1,-1)

NATURAL(Phi)=0 LINE TO (1,1)

VALUE(Phi)=1 LINE TO (-1,1)

NATURAL(Phi)=0 LINE TO CLOSE

LIMITED REGION 2 'blob' { the embedded blob }

LAYER 2 K = 0.001

START 'ring' (RSphere,0)

ARC(CENTER=0,0) ANGLE=360

TO CLOSE

PLOTS

GRID(y,z) on x=0

CONTOUR(Phi) on x=0

VECTOR(-k*grad(Phi)) on x=0

ELEVATION(Phi) FROM (0,-1,0) to (0,1,0)

END

Cut-away and cross-section images of the LAYER x REGION compartment structure of this layout looks like this:

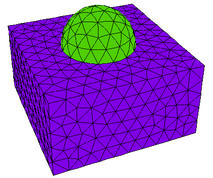
The contour plot looks like this:

Notice that because of the symmetry of the 3D figure, this plot looks like a rotation of the 2D contour plot in "Putting It All Together".

Shaped Layer Interfaces

Shaped Layer Interfaces